

The first computations of p-values were calculated by Pierre-Simon Laplace as far back as the late 18th century.

When data is not Normally distributed we can either transform the data (for example, by taking logarithms) and apply parametric tests or use non-parametric tests which do not require the data to be normally distributed for analysis. Binomial Distribution for binary categorical data in Survival Analysis, Chi Square Distribution in Chi Square test, t distribution in the t-test, and so on).Īlthough the sub-type of distribution influences the test of significance chosen, conventionally, data distributions that are not Normal, are not actually tested for the type of distribution prior to applying a statistical test. These distributions are useful for performing specific analysis of data and some of these will be discussed in the forthcoming articles (e.g. Just like the data which they describe, distributions can be classified as continuous or discrete. There are a large number of distributions that describe data as shown in Table 1 that are not " Normal". The Shapiro-Wilk test provides better power than the K-S test and has been recommended by some as the best choice for testing the normality of data.1 When Data is not Normally Distributed These tests compare the scores in the sample to a Normally distributed set of scores with the same mean and standard deviation. The K-S and Shapiro-Wilk tests are the commonly used tests. Several tests are available to assess Normality and include the Kolmogorov-Smirnov (K-S) test, Lilliefors corrected K-S test, Shapiro-Wilk test, Anderson-Darling test, Cramer-von Mises test, D'Agostino skewness test, Anscombe-Glynn kurtosis test, D'Agostino-Pearson omnibus test, and the Jarque-Bera test. Prior to expressing data as mean/median and to decide what tests can be applied to analyse data for statistical significance, it is necessary to identify whether the data is Normally distributed or not (for the reasons described above). Tests to Assess Normality of Distribution
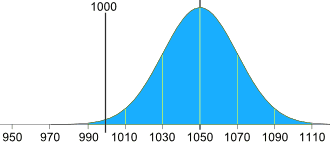
Normally distributed data while if the data is not Normally distributed, then non-parametric tests of significance should be employed to find a statistical difference. Further, parametric tests can be used to analyse. Rather, median and range/interquartile range are used to describe this type of data. Conversely, if the data is not Normally distributed it should NEVER be described as mean ± SD. If the data is Normally distributed, then it should always be described as mean ± SD. Importantly, the mean, median and mode are very close to each other. For example, if there is a sample of values of HbA1C levels of 1000 people, which is "Normally distributed", it means that there are 500 values below and 500 above the mean (Figure 1). The data is spread evenly and equally around the central value (which is the "mean") with 50% of data falling on either side of the mean. The distribution is dense at the centre and less dense at its tails. The area of one SD on either side represents 68% of the population, 2SD on either side 95% of the population and 3SD 99% of the population.Ĥ. The area under the Normal curve is 1.0 (100%) and is divisible for the purpose of analysis as in point 3ģ. These include the following:ġ.Ğvery Normal distribution is characterized by its mean and standard deviation.Ģ. oncology.Ī Normal distribution has several properties that make it useful for inferential statistics. Medicine, Normal distributions are rare e.g. Although manyīiological phenomena are Normally distributed, in some specialties in Statisticians use a capital N to emphasise this.
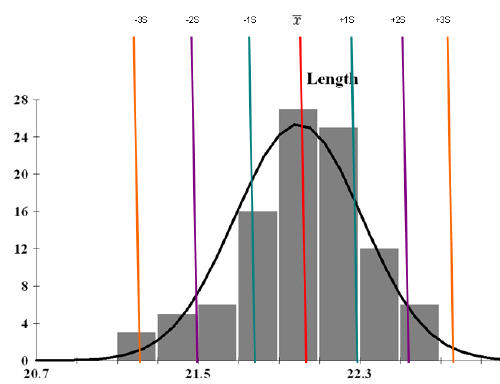
It is useful to note that the word "Normal"ĭoes not indicate that it is "normal" (as against abnormal) and The "Gaussian" distribution after the German mathematician Karlįriedrich Gauss (1777 1855). The "Normal Distribution" is probably the most important and most widely Statistical tests so that correct conclusions may be drawn. Meaningful information and also influences the choice of the appropriate That the values form after they are organised" and this is called aĭistribution. A distribution guides how raw data can be converted into The mean for the standard normal distribution is zero, and the standard deviation is one.When data is collected, in order to make sense of it, the data needs toīe organised in a manner which shows the various values and theįrequencies at which these values have occurred, that is the "pattern For example, if the mean of a normal distribution is five and the standard deviation is two, the value 11 is three standard deviations above (or to the right of) the mean. A z-score is measured in units of the standard deviation. The standard normal distribution is a normal distribution of standardized values called z-scores.


 0 kommentar(er)
0 kommentar(er)
